Answer:
a) Sample mean = 9.99
Sample standard deviation = 0.3348
b) -1.0389
c) 0.1631
Explanation:
We are given the following in the question:
9.7, 9.9, 10.3, 10.1, 10.5, 9.4, 9.9, 10.1, 9.7, 10.3
a) sample mean and standard deviation
Formula:
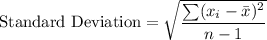
where
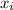 are data points,
are data points,
 is the mean and n is the number of observations.
is the mean and n is the number of observations.

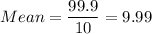
Sum of squares of differences = 1.009
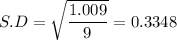
b) observed value of the t-statistic
Formula:
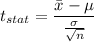
Putting all the values, we have
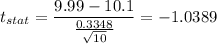
c) probability of these statistics (or worse) if the true mean were 10.1 mm
Degree of freedom = n - 1 = 9
Calculating the value from the table
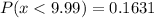
0.1631 is the the probability of these statistics (or worse) if the true mean were 10.1 mm