Question

A fuse in an electric circuit is a wire that is designed to melt, and thereby open the circuit, if the current exceeds a predetermined value. Suppose that the material to be used in a fuse melts when the current density rises to 480 A/cm2. What diameter of cylindrical wire should be used to make a fuse that will limit the current to 0.75 A

Answer 1

The diameter of the cylindrical wire is 0.0446 cm or 44.6 mm

Step-by-step explanation:

Given;

current density of the fuse, J = 480 A/cm²

current in the fuse, I = 0.75 A

Current density, J = Current (I) / Area (A)

`Area \ of \ the \ cylindrical \ wire = (Current \ (I))/(Current \ density \ (J)) = (0.75)/(480) = 1.5625*10^(-3) \ cm^2`

`Area \ of \ the \ cylindrical \ wire, A = (\pi d^2)/(4) \\\\d^2 =(4*A)/(\pi ) \\\\d = \sqrt{(4*A)/(\pi ) } = \sqrt{(4*1.5625*10^(-3))/(\pi ) }= 0.0446 \ cm =44.6 \ mm`

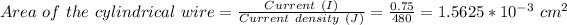
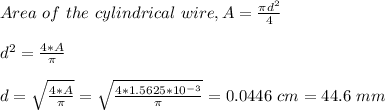
diameter of the wire = 0.0446 cm or 44.6 mm

Therefore, the diameter of cylindrical wire that should be used to make a fuse that will limit the current to 0.75 A, when the current density rises to 480 A/cm² is 44.6 mm