Answer:
Option D) s = 1
Explanation:
We are given the following information in the question:
Mean, μ = 69
X = 68
Formula:

Computing z-scores for different standard deviation:
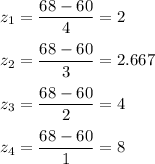
The standard deviation with highest z-score gives the most extreme position in the distribution.
Thus, the most extreme position of X = 68 in the distribution is given by a standard deviation of 1.
Option D) s = 1