Question

Oil having a specific gravity of 0.9 is pumped as illustrated with a water jet pump. The water volume flowrate is 1 m3 /s. The water and oil mixture has an average specific gravity of 0.95. Calculate the rate, in m3 /s, at which the pump moves oil.

Answer 1

The rate at which the pump moves oil is 1 m³/s

Step-by-step explanation:

Assumptions:

• there is steady-state flow

• oil and water are incompressible

• first fluid is water, second fluid is oil and third fluid is the mixture of oil and water.

`\rho_1Q_1 + \rho_2Q_2 = \rho_3Q_3 -------equation (i)`

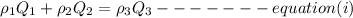
where;

ρ is the fluid density

Q is the volumetric flow rate

`Q_1 + Q_2 = Q_3--------equation (ii)`

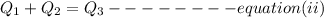
Substitute in Q₃ in equation i

`\rho_1Q_1 + \rho_2Q_2 = \rho_3(Q_1 +Q_2)`

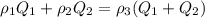
divide through by ρ₁

`(\rho_1Q_1)/(\rho_1)+ (\rho_2Q_2)/(\rho_1) =( \rho_3(Q_1 +Q_2))/(\rho_1)\\\\Note; (\rho_2)/(\rho_1) = \gamma_2 \ and \ (\rho_3)/(\rho_1) = \gamma_3\\\\Q_1 + \gamma_2Q_2 = \gamma_3(Q_1+Q_2)`

Make Q₂ the subject of the formula

`Q_2 = (Q_1(1- \gamma_3))/(\gamma_3-\gamma_2) = (1 ((m^3)/(s)) (1-0.95))/(0.95-0.9) = 1 \ (m^3)/(s)`

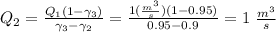
Therefore, the rate at which the pump moves oil is 1 m³/s