Answer:
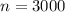 seeds planted in the farm
seeds planted in the farm
From these 3000 we know that only 2200 germinated
In order to determine the probability that a seed will germinate we can use the definition of probability given by:
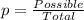
From this definition we need to divide the possible cases by the total cases and for this case if we replace we got:
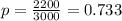
So then the probability that the seed will germinate is 0.733 from the sample data obtained
Explanation:
For this case we know that the sample size is:
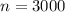 seeds planted in the farm
seeds planted in the farm
From these 3000 we know that only 2200 germinated
In order to determine the probability that a seed will germinate we can use the definition of probability given by:
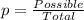
From this definition we need to divide the possible cases by the total cases and for this case if we replace we got:
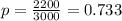
So then the probability that the seed will germinate is 0.733 from the sample data obtained