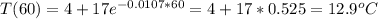Question

An object is taken out of a 21 degree C room and placed outside where the temperature is 4 degree C. Twenty-five minutes later the temperature is 17 degree C. It cools according to Newton's Law. Determine the temperature of the object after one hour. Round to the nearest tenth of a degree.

Answer 1

12.9 degree C

Explanation:

1 hour = 60 minutes

So the Newton's law of cooling state that the rate of changing in temperature is proportional to the different in temperature, in other words:

`(dT)/(dt) = -k(T - T_e)`

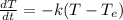
where t is the time in minute, k is the cooling constant and
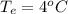`T_e = 4^o C` is the environmental temperature. This differential equation can be solved to have a form of

`T(t) = T_e + (T_0 - T_e)e^(-kt)`

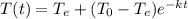
where
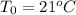`T_0 = 21^o C` is the initial temperature.

We know that at 25 minutes T(25) = 17

`4 + (21 - 4)e^(-25k) = 17`

`4 + 17e^(-25k) = 17`

`e^(-25k) = (17 - 4)/17 = 0.765`

`-25k = ln(0.765) = -0.268`

`k = -0.268 / -25 = 0.0107`

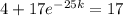
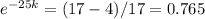
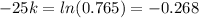
So after 60 minutes:

`T(60) = 4 + 17e^(-0.0107*60) = 4+17*0.525 = 12.9 ^o C`

Answer 2

Answer: The temperature of the object after one hour is 12.9°C to the nearest tenth of a degree

Explanation:

Please see the attachments below