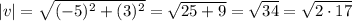Answer:
Explanation:
The magnitude of a vector is the length of the vector itself.
Given a bi-dimensional vector, the magnitude of the vector is given by:
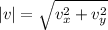
where
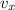 is the x-component of the vector
is the x-component of the vector
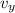 is the y-component of the vector
is the y-component of the vector
The vector in this problem is
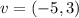
Therefore its components are
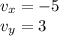
And so, the magnitude of the vector is: