Question

The level of nitrogen oxides (NOX) in the exhaust after 50,000 miles or fewer of driving of cars of a particular model varies Normally with mean 0.02 g/mi and standard deviation 0.01 g/mi. A company has 81 cars of this model in its fleet. What is the level L such that the probability that the average NOX level x for the fleet is greater than L is only 0.01? (Hint: This requires a backward Normal calculation. Round your answer to three decimal places.)

Answer 1

For a level of 0.0174 or more of nitrogen oxide, the probability of fleet is 0.01.

Explanation:

We are given the following information in the question:

Mean, μ = 0.02 g/mi

Standard Deviation, σ = 0.01 g/mi

Sample size, n = 81

We are given that the distribution of level of nitrogen oxides is a bell shaped distribution that is a normal distribution.

Standard error due to sampling:

`=(\sigma)/(√(n)) = (0.01)/(√(81)) = 0.0011`

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

We have to find the value of x such that the probability is 0.01

P(X > x)

`P( X > x) = P( z > \displaystyle(x - 0.02)/(0.0011))=0.01`

`= 1 -P( z \leq \displaystyle(x - 0.02)/(0.0011))=0.01`

`=P( z \leq \displaystyle(x - 0.02)/(0.0011))=0.99`

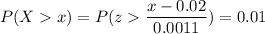
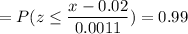
Calculation the value from standard normal z table, we have,

`\displaystyle(x - 0.02)/(0.0011) = -2.326\\\\x = 0.0174`

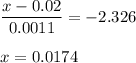
For a level of 0.0174 or more of nitrogen oxide, the probability of fleet is 0.01.