Question

An investment analyst has tracked a certain bluechip stock for the past six months and found that on any given day, it either goes up a point or goes down a point. Furthermore, it went up on 25% of the days and down on 75%. What is the probability that at the close of trading four days from now, the price of the stock will be the same as it is today? Assume that the daily fluctuations are independent event

Answer 1

0.2109 or 21.09%

Explanation:

In order to maintain the same price after two days, the stock must go up (U) on two days and go down (D) on two days, the sample space for this event is:

S={UUDD, UDUD, UDDU, DDUU, DUDU, DUUD}

There are 6 equally likely possible outcomes. The probability that the price of the stock will be the same as it is today is:

`P =6* (0.25*0.25*0.75*0.75)\\P=0.2109=21.09\%`

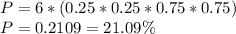
The probability is 0.2109 or 21.09%.