Question

Suppose that the linear density of the A string on a violin is 8.20 10-4 kg/m. A wave on the string has a frequency of 410 Hz and a wavelength of 71 cm. What is the tension in the string?

Answer 1

T = 69.49 N

Step-by-step explanation:

The relation between the tension and speed of a wave is:

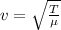`v=\sqrt{(T)/(\mu)}` (1)

Where:

• T is the tension of the string
• μ is the linear density (8.20*10⁻⁴ kg/m)
• v is the speed of the wave

Let's recall, that the speed of a wave is the wavelength times the frequency, so:

`v=\lambda *f=0.71*410=291.1 m/s`

Now, we just need to solve the equation (1) for T and use the value of v we found before.

`T=\mu v^(2)=8.20*10^(-4)*(291.1)^(2)=69.49 N`

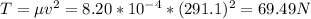
Therefore the tension of string is 69.49 N.

I hope it helps you!