Question

Given that z is a standard normal random variable, find z for each situation. The area between 0 and z is .4750. Answer The area between 0 and z is .2291. Answer The area to the right of z is .1314. Answer The area to the left of z is .6700.

Answer 1

`P(0<Z<z) =P(Z<z)-P(Z<0) = P(Z<z)-0.5= 0.4750`

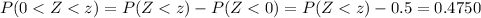
And solving for z we have

`P(Z<z)= 0.4750+0.5= 0.9750`

And we can find the value for z with the following excel code:

"=NORM.INV(0.975,0,1)"

And we got z =1.96

`P(Z>z)= 0.1314`

And we can use the complement rule and we got:

`P(Z>z) = 1-P(Z<z) = 0.1314`

`P(Z<z)= 1-0.1314= 0.8686`

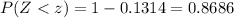
And we can find the value for z with the following excel code:

"=NORM.INV(0.8686,0,1)"

And we got z =1.120

`P(Z<z)= 0.67`

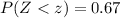
And we can find the value for z with the following excel code:

"=NORM.INV(0.67,0,1)"

And we got z =0.440

Explanation:

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".

Solution to the problem

We want this probability:

`P(0<Z<z) =P(Z<z)-P(Z<0) = P(Z<z)-0.5= 0.4750`

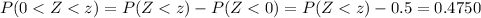
And solving for z we have

`P(Z<z)= 0.4750+0.5= 0.9750`

And we can find the value for z with the following excel code:

"=NORM.INV(0.975,0,1)"

And we got z =1.96

For the next part we want to calculate:

`P(Z>z)= 0.1314`

And we can use the complement rule and we got:

`P(Z>z) = 1-P(Z<z) = 0.1314`

`P(Z<z)= 1-0.1314= 0.8686`

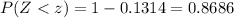
And we can find the value for z with the following excel code:

"=NORM.INV(0.8686,0,1)"

And we got z =1.120

For the next part we want to calculate:

`P(Z<z)= 0.67`

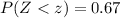
And we can find the value for z with the following excel code:

"=NORM.INV(0.67,0,1)"

And we got z =0.440