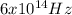Question

The speed of light is about 3.00 × 10 meters per second. What is the frequency of green light that has a wavelength about 500 nanometers? (1 nm = 10 m)

Answer 1

The frequency of the green light is
`6x10^(14)Hz`

Step-by-step explanation:

The visible region is part of the electromagnetic spectrum, any radiation of that electromagnetic spectrum has a speed of
`3.00x10^(8)m/s` in the vacuum.

Green light is part of the visible region. Therefore, the frequency can be determined by the following equation:

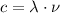`c = \lambda \cdot \\u` (1)

Where c is the speed of light,
`\lambda` is the wavelength and
`\\u` is the frequency.

Notice that since it is electromagnetic radiation, equation 1 can be used. Remember that light propagates in the form of an electromagnetic wave (that is a magnetic field perpendicular to an electric field).

Then,
`\\u` can be isolated from equation 1

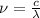`\\u = (c)/(\lambda)` (2)

Notice that it is necessary to express the wavelength in units of meters.

`\lambda = 500nm . (1m)/(1x10^(9)nm)` ⇒
`5x10^(-7)m`

`\\u = (3.00x10^(8)m/s)/(5x10^(-7)m)`

`\\u = 6x10^(14)s^(-1)`

`\\u = 6x10^(14)Hz`

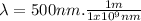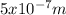
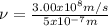
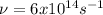
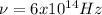
Hence, the frequency of the green light is
`6x10^(14)Hz`