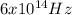Answer:
The frequency of the green light is
Step-by-step explanation:
The visible region is part of the electromagnetic spectrum, any radiation of that electromagnetic spectrum has a speed of
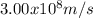 in the vacuum.
in the vacuum.
Green light is part of the visible region. Therefore, the frequency can be determined by the following equation:
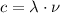 (1)
(1)
Where c is the speed of light,
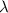 is the wavelength and
is the wavelength and
 is the frequency.
is the frequency.
Notice that since it is electromagnetic radiation, equation 1 can be used. Remember that light propagates in the form of an electromagnetic wave (that is a magnetic field perpendicular to an electric field).
Then,
 can be isolated from equation 1
can be isolated from equation 1
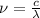 (2)
(2)
Notice that it is necessary to express the wavelength in units of meters.
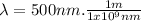 ⇒
⇒
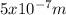
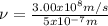
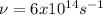
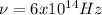
Hence, the frequency of the green light is