The total area of the entire wall = 440 sq feet.
Explanation:
Here, let us assume:
The total number of tiles = T
The total number of jumbo tiles = J
The total number of regular tiles = J
⇒ R + J = T or, R + J = 3 J
⇒ R = 3J - J
⇒ R = 2 J
⇒ J =

Now, let us assume the length of regular tile = L
And the width of the regular tile = W
So, the area of 1 regular tile = Length x Width = L x W =
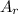
So, the length of the jumbo tile = 3 x ( Length of Regular tile ) = 3 L
⇒The width of the jumbo tile = 3 x ( width of Regular tile ) = 3 W
So, the area of 1 jumbo tile = Length x Width = (3 L) x (3 W) =
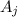
= 9 L W = 9 (Area of 1 regular tile) = 9
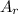
⇒
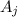 = 9
= 9
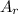
Now, the total area of regular tiles = 80 sq ft
So, Number of regular tiles x Area of 1 regular tile = 80 sq ft
Now, the total area A = Number of jumbo tiles x Area of each jumbo tile + Number of regular tiles x Area of each regular tile
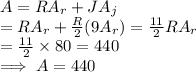
Hence, the total area of the entire wall = 440 sq feet.