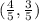Question

The masses mi are located at the points Pi. Find the moments Mx and My and the center of mass of the system. m1 = 4, m2 = 3, m3 = 3; P1(2, −3), P2(−3, 1), P3(3, 5)

Answer 1

`M_x`= 8

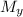`M_y` = 6

Therefore the co-ordinate of the center of mass is =
`((4)/(5),(3)/(5))`

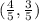
Explanation:

Center of mass: Center of mass of an object is a point on the object. Center of mass is the average position of the system.

Center of mass of a triangle is the centriod of a triangle.

Given that m₁= 4, m₂=3, m₃=3 and the points are P₁(2,-3), P₂(-3,1) and P₃(3,5)

`M_x` = ∑(mass × x-co-ordinate)

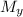`M_y` = ∑(mass × y-co-ordinate)

Therefore

`M_x` = (4×2)+{3×(-3)}+(3×3)

=8

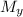`M_y` = {4×(-3)}+{3×1}+(3×5)

=6

The x co-ordinate of the center of mass is the ratio of
`M_x` to the total mass.

The y co-ordinate of the center of mass is the ratio of
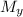`M_y` to the total mass.

Total mass (m) = m₁+ m₂+ m₃

= 4+3+3

=10

The x co-ordinate of the center of mass is
`\frac {8}{10} = \frac {4}{5}`

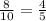
The y co-ordinate of the center of mass is
`(6)/(10)=(3)/(5)`

Therefore the co-ordinate of the center of mass is =
`((4)/(5),(3)/(5))`