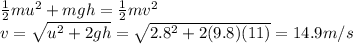Question

A skateboarder with a mass of 82 kg traveling at 2.8 m/s approaches a hill and rides down it. The hill is 11 m high. Assuming a complete transformation of mechanical energy into kinetic energy, what is the skateboarder's velocity at the bottom of the hill? v f = m / s

Answer 1

14.9 m/s

Step-by-step explanation:

At the top of the hill, the skateboarder has both kinetic energy and potential energy, so its total mechanical energy is:

`E=K_i+U_i = (1)/(2)mu^2 +mgh`

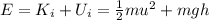
where

m = 82 kg is the mass of the skateboarder

u = 2.8 m/s is the initial velocity

`g=9.8 m/s^2` is the acceleration due to gravity

h = 11 m is the initial height of the skateboarder

At the bottom of the hill, all the energy has been converted into kinetic energy, so:

`E=K_f = (1)/(2)mv^2`

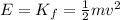
where

v is the final velocity of the skateboarder

Since the mechanical energy must be conserved, we can equate the two energies, and find the final velocity:

`(1)/(2)mu^2 +mgh=(1)/(2)mv^2\\v=√(u^2+2gh)=√(2.8^2+2(9.8)(11))=14.9 m/s`