Answer:
Explanation:
Hello!
The study variable is:
X: number of customers that recognize a new product out of 120.
There are two possible recordable outcomes for this variable, the customer can either "recognize the new product" or " don't recognize the new product". The number of trials is fixed, assuming that each customer is independent of the others and the probability of success is the same for all customers, p= 0.6, then we can say this variable has a binomial distribution.
The sample proportion obtained is:
p'= 54/120= 0.45
Considering that the sample size is large enough (n≥30) you can apply the Central Limit Theorem and approximate the distribution of the sample proportion to normal: p' ≈ N(p;
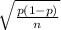 )
)
The other conditions for this approximation are also met: (n*p)≥5 and (n*q)≥5
The probability of getting the calculated sample proportion, or lower is:
P(X≤0.45)= P(Z≤
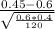 )= P(Z≤-3.35)= 0.000
)= P(Z≤-3.35)= 0.000
This type of problem is for the sample proportion.
I hope this helps!