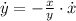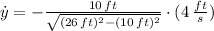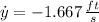Question

A 26 ft ladder leaning against a wall begins to slide. How fast is the top of the ladder sliding down the wall at the instant of time when the bottom of the ladder is 10 ft from the wall and sliding away from the wall at the rate of 4 ft/sec?

Answer 1

`\dot y = -1.667\,(ft)/(s)`

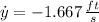
Step-by-step explanation:

Let consider positive when top of the ladders slides up and the bottom of the ladder slides away from the wall. Ladder can be described by Pythagorean Theorem:

`r^(2) = x^(2) + y^(2)`

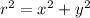
Where:

`r` is the ladder length,
`x` is the horizontal distance between the bottom of the ladder and wall and
`y` is the vertical distance between floor and the top of the ladder.

An expression describing velocities at top and bottom of the ladder can be obtained by using derivatives as a function of time:

`2\cdot x \cdot \dot x\, + 2\cdot y \cdot \dot y = 0`

`x\cdot \dot x\, + y \cdot \dot y = 0`

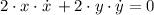
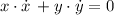
The rate for the top of the ladder is:

`\dot y = - (x)/(y)\cdot \dot x`

`\dot y = -\frac{10\,ft}{\sqrt{(26\,ft)^(2)-(10\,ft)^(2)} } \cdot (4\,(ft)/(s) )`

`\dot y = -1.667\,(ft)/(s)`