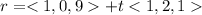Answer:
the parameter equation of given line is
x= 1+t
y=0+ 2t
z= 9+t
( note: in plane no signs given so we assume + so x+2y+z)
Explanation:
A vector perpendicular to the plane a x + b y + c z + d = 0 is given by ⟨ a , b , c ⟩
So a vector perpendicular to the plane x +2 y + z − = 0 is ⟨ 1 , 2 , 1 ⟩
The parametric equation of a line through
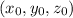 and parallel to the vector ⟨ a , b , c ⟩ is
and parallel to the vector ⟨ a , b , c ⟩ is
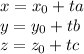
so the parametric equation of our line is
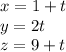
The vector form of the line is