Question

Multiply: 4x * root(3, 4x ^ 2) * (2 * root(3, 32x ^ 2) - x * root(3, 2x))

Answer 1

`32x^2\sqrt[3]{2x} -8x^3`

Explanation:

To multiply radicals of the same index, we multiply the coefficient of the radicals together and the radicands (the things inside the radical) together.

`4x\sqrt[3]{4x^2} (2\sqrt[3]{32x^2} -x\sqrt[3]{2x} )`

`(4x)(2)\sqrt[3]{(4x^2)(32x^2)} -(4x)(x)\sqrt[3]{(4x^2)(2x)}`

`8x\sqrt[3]{128x^4} -4x^2\sqrt[3]{8x^3}`

Remember that
`128=2^7=(2^6)(2)`,
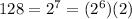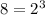`8=2^3`, and
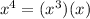`x^4=(x^3)(x)`, so:

`8x\sqrt[3]{(2^6)(2)(x^3)(x)} -4x^2\sqrt[3]{2^3x^3}`

Remember that radicands with the same index (or evenly divisible by the index) can be taken out the radical, so:

`(2^2)(x)(8x)\sqrt[3]2{x} -(4x^2)(2x)`

`32x^2\sqrt[3]{2x} -8x^3`

We can conclude that the second choice is the correct answer.

Answer 2

`32 {x}^(2) \sqrt[3]{ 2x } -8{x}^(3)`

Explanation:

We want to

`4x \sqrt[3]{4 {x}^(2) } (2 \sqrt[3]{32 {x}^(2) } - x \sqrt[3]{2x} )`

We expand to obtain:

`4x \sqrt[3]{4 {x}^(2) } * 2 \sqrt[3]{32 {x}^(2) } -4x \sqrt[3]{4 {x}^(2) } * x \sqrt[3]{2x} )`

We now simplify

`8x \sqrt[3]{4 {x}^(2) * 32 {x}^(2) } -4 {x}^(2) \sqrt[3]{4 {x}^(2) * 2x}`

We multiply the radicand

`8x \sqrt[3]{64 * {x}^(3) * 2x } -4 {x}^(2) \sqrt[3]{8 {x}^(3)}`

Or

`8x \sqrt[3]{ {(4x)}^(3) * 2x } -4 {x}^(2) \sqrt[3]{{(2x)}^(3)}`

We take cube root to get:

`8x * 4x\sqrt[3]{ 2x } -4 {x}^(2) * 2x`

We multiply out to get:

`32 {x}^(2) \sqrt[3]{ 2x } -8{x}^(3)`