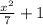Question

Is x^2/7+1 a polynomial

Answer 1

`(x^(2))/(7)+1` is a polynomial .

Explanation:

We have , the following expression x^2/7+1 ,i.e.
`(x^(2))/(7)+1`.

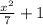A polynomial function is a function such as a quadratic, a cubic, a quadratic, and so on, involving only non-negative integer powers of x. Some examples are :

f(x)=3x−2 Linear polynomial (linear function)

f(x)=
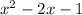`x^(2)-2x-1` Quadratic polynomial

f(x)=−
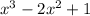`x^(3)-2x^(2)+1` Cubic polynomial with no quadratic term

f(x)=(x−3)2(2x−1)

A polynomial of degree n is a function of the form:

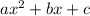`ax^(2)+bx+c` for a quadratic polynomial , here equation :

⇒
`(x^(2))/(7)+1`

⇒
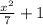
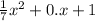`(1)/(7)x^(2)+ 0.x+ 1` which is equivalent to
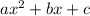`ax^(2)+bx+c`.Hence,
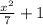`(x^(2))/(7)+1` is a polynomial .