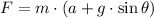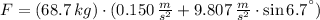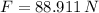Answer:
a)
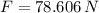 , b)
, b)
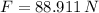
Step-by-step explanation:
a) Let consider two equations of equilibrium, the first parallel to ski slope and the second perpendicular to that. The equations are, respectively:
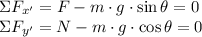
The force on the skier is:
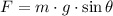
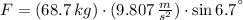
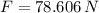
b) The equations of equilibrium are the following:
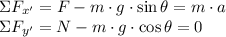
The force on the skier is: