Question

A toy company can spend no more than $2,000 on raw materials for plastic trains and metal trains. The raw materials cost $0.80 per pound for metal and $0.40 per pound for plastic. To summarize the situation, a worker writes the inequality: 0.8m + 0.4p ≤ 2,000, where m is the number of pounds of metal material and p is the number of pounds of plastic material. Which graph's shaded region shows the possible combinations of raw materials the company can buy?

Answer 1

The shaded region on the graph below, where the inequality
`\(0.8m + 0.4p \leq 2,000\)` is satisfied, represents the possible combinations of pounds of metal (m) and plastic (p) materials the toy company can buy.

The given inequality
`\(0.8m + 0.4p \leq 2,000\)` represents the budget constraint for the toy company, indicating that the total cost of the raw materials (metal and plastic) must not exceed $2,000. To graphically represent this constraint, we can rearrange the inequality to solve for (p):
`\[0.4p \leq 2,000 - 0.8m.\]` Dividing both sides by 0.4 yields
`\(p \leq 5,000 - 2m\),` which is the slope-intercept form of the inequality.

The graph of this inequality is a line with a slope of -2 and a y-intercept of 5,000. However, since (p) cannot be negative, we consider only the region where (p) is non-negative. The shaded region below the line represents the combinations of pounds of metal (m) and plastic (p) materials that satisfy the budget constraint.

In conclusion, the graph visually illustrates the feasible region for the toy company's raw material purchase, ensuring that the total cost does not exceed $2,000. The shaded area below the line reflects the valid combinations of pounds of metal and plastic materials, allowing the company to stay within its budgetary constraints.

Answer 2

The gaph is shown in the image below

Explanation:

Graph of Inequalities

Let's graph the region of the inequality

`0.8m + 0.4p \leq 2,000`

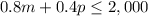
Since there is no indication, we'll assume the variable p to be in the horizontal axis and m in the vertical axis. Let's solve for m

`\displaystyle m=(2,000-0.4p)/(0.8)`

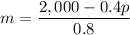
Since both m and p are positive, we can assume

`2,000-0.4p\geq 0`

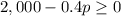
Or, equivalently

`p \leq 5,000`

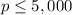
Thus, we can give p any value between 0 and 5,000 to get the corresponding values for m. Let's select the values p=0, p=1,000, p=5,000 to get the points

( 0 ; 2,500 ) ( 1,000 ; 2,000 ) ( 5,000 ; 0 )

With these points we can plot the line representing the function. To know which area must be shaded, we only need to test one point below or above the line. If it fulfills the inequality, then the whole area is shaded.

Let's test the point ( 1,000 ; 1,000 )

`0.8\cdot 1,000 + 0.4\cdot 1,000 \leq 2,000`

`1,200 \leq 2,000`

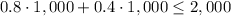
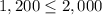
Since the condition is met, the area below the line must be shaded as the solution of the inequality

The gaph is shown in the image below