Question

solve the following systems of equations express the answer as an ordered pair in the format (a,b) with no spaces between the numbers or symbols 2x7y=-7 and -4x-3y=-19

Answer 1

(7, -3)

Explanation:

The correct system is 2x+7y=-7 and -4x-3y=-19.

Equation (1) will be
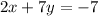`2x+7y=-7`, and equation (2)
`-4x-3y=-19`

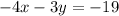
Let's solve our system of equations using elimination:

Step 1. Multiply equation (1) by 2 and add the result to equation (2) and solve for y

4x + 14y = -14) +

-4x - 3y = -19

‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾

11y = -33

`y=(-33)/(11)`

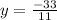
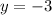`y=-3` equation (3)

Step 2. Replace equation (3) in equation (1) and solve for x

`2x+7y=-7`

`2x+7(-3)=-7`

`2x-21=-7`

`2x=14`

`x=7`

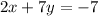
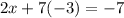
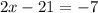
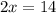
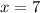
We can conclude that the solution of the system of equations is (7, -3)