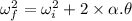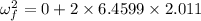Question

A uniform disk with mass 38.7 kg and radius 0.240 m is pivoted at its center about a horizontal, frictionless axle that is stationary. The disk is initially at rest, and then a constant force 30.0 N is applied tangent to the rim of the disk.What is the magnitude v of the tangential velocity of a point on the rim of the disk after the disk has turned through 0.320 revolution?

Answer 1

`\omega_f=5.097\ rad.s^(-1)`

Step-by-step explanation:

Given:

• mass of uniform disk,
  `m=38.7\ kg`

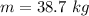
• radius of the disk,
  `r=0.24\ m`

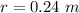
• initial velocity of the disk,
  `\omega_i=0\ rad,s^(-1)`

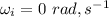
• magnitude of the force acted upon the rim of the disk,
  `F=30\ N`

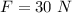
• angular displacement of the disk,
  `\theta=0.32* 2\pi=2.011\ rad`

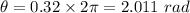
Moment of inertia of the given disk:

`I=(1)/(2)* m.r^2`

`I=0.5* 38.7* 0.24^2`

`I=1.11456\ kg.m^2`

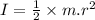
Also the torque due to the force is given as:

`\tau=F* r`

`\tau=30* 0.24`

`\tau=7.2\ N.m`

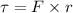
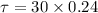
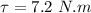
Torque in terms of angular acceleration:

`\tau=I.\alpha`

`\alpha=(\tau)/(I)`

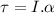
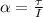
where:

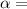`\alpha=` angular acceleration

`\alpha=(7.2)/(1.11456)`

`\alpha=6.4599\ rad.s^(-2)`

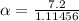
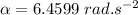
Now using the equation of motion:

`\omega_f^2=\omega_i^2+2* \alpha.\theta`

`\omega_f^2=0+2* 6.4599* 2.011`

`\omega_f=5.097\ rad.s^(-1)`