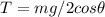Answer:
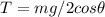
Explanation:
#Given that each rope is tied to the cylinder top and makes the same
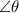 with the vertical,:
with the vertical,:
Let tension on the rope be
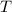
#The vertical component of each T is,
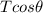
Total vertical component is
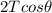
We know that
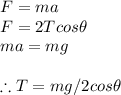 #where
#where
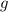 is gravitational acceleration.
is gravitational acceleration.
Hence the tension of each rope is