Question

Consider the following linear programming problem: Max Z = $200x1 + $100x2 Subject to: 8x1 + 5x2 ≤ 80 2x1 + x2 ≤ 100 x1, x2 ≥ 0 What is maximum Z and the value of x1 and x2 at the optimal solution?

Answer 1

The maximum value of Z is 2,000 for x_1=10 and x_2=0

Explanation:

we have

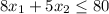`8x_1+5x_2\leq 80` -----> inequality A

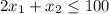`2x_1+x_2\leq 100` -----> inequality B

`x_1\geq 0` -----> inequality C

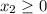`x_2\geq 0` -----> inequality D

Solve the system of inequalities by graphing

The solution is the triangular shaded area

see the attached figure

The vertices of the shaded area are

(0,0),(0,16) and (10,0)

we have

`Z=200x_1+100x_2`

To find out the maximum value of Z, substitute the value of x_1 and the value of x_2 of each vertex and then compare the results

`For\ (0,0) ----> Z=200(0)+100(0)=0`

`For\ (0,16) ----> Z=200(0)+100(16)=1,600`

`For\ (10,0) ----> Z=200(10)+100(0)=2,000`

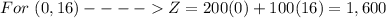
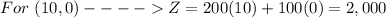
therefore

The maximum value of Z is 2,000 for x_1=10 and x_2=0