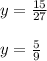Answer:

Explanation:
It is important to remember that an Exponential function has the following form:
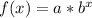
Where “b” is
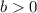 and
and
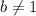 , "a" is a coefficient, "x" is the Independent variable and f(x) is the Dependent variable.
, "a" is a coefficient, "x" is the Independent variable and f(x) is the Dependent variable.
In this case, you have the following Exponential Function given in the exercise:
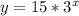
If the value of Dependent variable is -3, then:

So, you must substitute that value of "x" into the function:
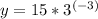
And now you must evaluate:
1. According the Negative exponent rule:
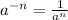
Then:
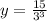
2. Simplifying, you get: