Question

Trevor is interested in purchasing the local hardware/sporting goods store in the small town of Dove Creek, Montana. After examining accounting records for the past several years, he found that the store has been grossing over $850 per day about 60% of the business days it is open. Estimate the probability that the store will gross over $850 for the following. (Round your answers to three decimal places.)(a) at least 3 out of 5 business days(b) at least 6 out of 10 business days(c) fewer than 5 out of 10 business days(d) fewer than 6 out of the next 20 business days.

Answer 1

a.0.6826

b.0.6330

c.0.1663

d.0.0016

Explanation:

a. The business sale's follows a binomial distribution which is defined by the formula:

`{n\choose x}p^x(1-p)^n^-^x\\\\\\n=5,10,20\\p=0.6, (1-p)=1-0.6=0.4`

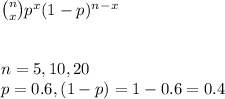
To find the probability of at least 3 out of 5, we sum the probabilities of 3 through 5:

`P(X=x)={n\choose x}p^x(1-p)^n^-^x\\\\P(X\geq 3)=P(X=3)+P(X=4)+P(X=5)={5\choose 3}0.6^3* 0.4^2+{5\choose 4}0.6^4* 0.4^1+{5\choose 5}0.6^5* 0.4^0\\=0.3456+0.2954+0.0778=0.6826`

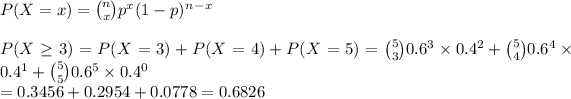
Hence the probability of at least 3/5 days is 0.6826

b. The probability of the store grossing over $850 on at least 6/10 business days follows a binomial distribution.

-Given n=10, p=0.6, our distribution can be expressed as:

`P(X=x)={n\choose x}p^x(1-p)^n^-^x\\P(\geq6)=P(X=6)+P(X=7)+P(X=8)+P(X=9)+P(X=10)\\\\={10\choose 6}0.6^6* 0.4^4+{10\choose 7}0.6^7* 0.4^3+{10\choose 8}0.6^8* 0.4^2+{10\choose 9}0.6^9* 0.4^1+{10\choose 10}0.6^1^0* 0.4^0\\\\=0.2508+0.2150+0.1209+0.0403+0.0060\\=0.6330`

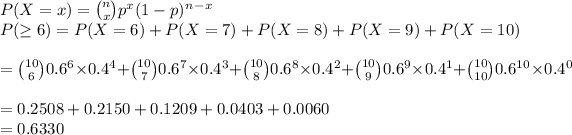
Hence the probability of at least 6 out of 10 days is 0.6330

c. The probability of the store grossing over $850 being fewer than 5 out of10 days:

Our variables are defined as n=10,p=0.6 and our distribution expressed as:

`P(X=x)={n\choose x}p^x(1-p)^n^-^x\\P(X<5)=P(X=0+X=1+X=2+X=3+X=4)\\={10\choose 0}0.6^0* 0.4^1^0+{10\choose 1}0.6^1* 0.4^9+{10\choose 2}0.6^2* 0.4^8+{10\choose 3}0.6^3* 0.4^7+{10\choose 4}0.6^4* 0.4^6\\=0.0001+0.0016+0.0106+0.0425+.1115\\=0.1663`

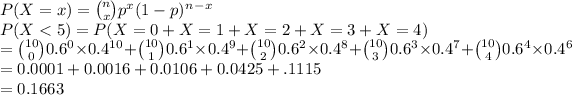
Hence there's a 0.1663 probability that fewer than 5/10 days grossed over $850.

d.The probability of the store grossing over $850 being fewer than 6 out of 20 days:

Our variables are defined as n=20,p=0.6 and our distribution expressed as:

`P(X=x)={n\choose x}p^x(1-p)^n^-^x\\P(X<6)=P(X=0+X=1+X=2+X=3+X=4+P=5)\\={20\choose 0}0.6^0* 0.4^2^0+{20\choose 1}0.6^1* 0.4^1^9+{20\choose 2}0.6^2* 0.4^1^8+{10\choose 3}0.6^3* 0.4^1^7+{20\choose 5}0.6^5* 0.4^1^5\\=0.0000+0.0000+0.0000+0.0000+0.0003+0.0013\\=0.0016`

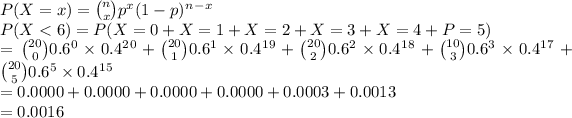
Hence there's a 0.0016 probability that fewer than 6/20days grossed over $850.