Question

In a murder investigation, the temperature of the corpse was 32.5°C at 1:30 pm and 30.3°C an hour later. Normal body temperature is 37.0°C and the temperature of the surroundings was 20.0°C. When did the murder take place?

Answer 1

Explanation:

Given that in a murder investigation, the temperature of the corpse was 32.5°C at 1:30 pm and 30.3°C an hour later.

Normal body temperature is 37.0°C and the temperature of the surroundings was 20.0°C.

As per Newton law of cooling we have

`T(t) = T_s+(T_0-T_s)e^(-kt)`

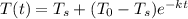
is the temperature at time t.

Substitute this for given two information to find k and T0

`32.5 = 20+(37-20)e^(-kt) \\30.3 = 20+(37-20)e^(-k(t+1))`

`12.5 = (17)e^(-kt) ...i\\10.3 =17e^(-k(t+1))...ii`

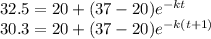
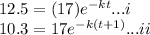
Divide I equation by II to get

`1.2136=e^k\\k = 0.1936`

Using this we find t at 1.30 p.m.

`32.5 = 20+(37-20)e^(-0.1936t) \\\\0.7353=e^(-0.1936t) \\t= 1.588`

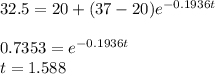
i.e. approximately 1.6 hours or 1 hour 36 minutes lapsed at 1.30

Time of murder is

11 hrs 54 minutes.