Question

A bus is traveling at 25 m/s, and a cyclist is traveling at 5 m/s behind the bus, in the same direction. the frequency of a sound coming from the bus is observed by the cyclist to be 1000 hz. approximately what is the frequency of the sound as perceived by the bus driver

Answer 1

Approximately
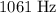`1061\; {\rm Hz}` (rounded to the nearest whole number,) assuming that the speed of sound in the air is
`330\; {\rm m \cdot s^(-1)}`.

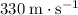Step-by-step explanation:

Let
`v` denote the speed of this sound wave:
`v = 330\; {\rm m\cdot s^(-1)}` by assumption.

Let
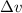`\Delta v` denote the speed at which the source (the bus) moves away from the observer (the cyclist.) In this question,
`\Delta v = 25\; {\rm m\cdot s^(-1)} - 5\; {\rm m\cdot s^(-1)} = 20\; {\rm m\cdot s^(-1)}`.

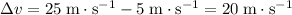Let
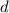`d` denote the distance between the source (the bus) and the observer (the cyclist) when the first crest leaves the source. At a speed of
`v`, it would take
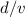`d / v` before the first crest arrive at the observer.

Let
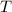`T` denote the period of this wave. If a crest of this wave leaves the source at
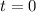`t = 0`, the very next one would leave at
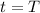`t = T`. Since the source is moving away from the observer at
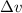`\Delta v`, the distance between the two would have since increased from
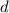`d` to
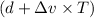`(d + \Delta v* T)`. At a speed of
`v`, this crest would now need
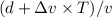`(d + \Delta v* T) / v` to reach the observer.

In summary:

• The first crest leaves the source at
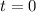  `t = 0` and arrives at the observer at
  `t = d / v`.
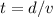• The second crest leaves the source at
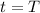  `t = T` and arrives at the observer at
  `t = T + (d + \Delta v* T) / v`.

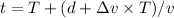The time difference between the two crests is
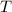`T` at the source. However, at the observer, this difference would have become:

`\begin{aligned} &T + (d + \Delta v* T)/(v) - (d)/(v) \\ =\; & T + (\Delta v* T)/(v) \\ =\; & T* (v + \Delta v)/(v)\end{aligned}`.

Therefore, the ratio between the period at the source and at the observer would be:

`\begin{aligned}\frac{T(\text{observer})}{T(\text{source})} &= (\displaystyle T * (v + \Delta v)/(v))/(T) \\ &= (v + \Delta v)/(v)\end{aligned}`.

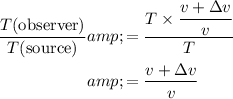The frequency
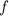`f` of a wave is equal to the reciprocal of its period
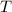`T`. In other words,
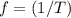`f = (1 / T)`. Therefore:

`\begin{aligned}\frac{f(\text{observer})}{f(\text{source})} &= \frac{T(\text{source})}{T(\text{observer})} \\ &= (v)/(v + \Delta v)\end{aligned}`.

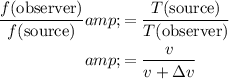Since
`f(\text{observer}) = 1000\; {\rm Hz}`,
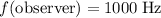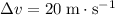`\Delta v = 20\; {\rm m\cdot s^(-1)}`, and
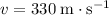`v = 330\; {\rm m\cdot s^(-1)` by assumption:

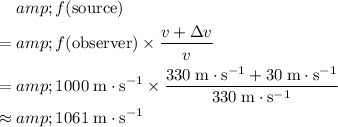`\begin{aligned} & f(\text{source})\\ =\; & f(\text{observer}) * (v + \Delta v)/(v) \\ =\; & 1000\; {\rm m\cdot s^(-1)} * \frac{330\; {\rm m\cdot s^(-1)} + 30\; {\rm m\cdot s^(-1)}}{330\; {\rm m\cdot s^(-1)}} \\ \approx\; & 1061\; {\rm m\cdot s^(-1)}\end{aligned}`.