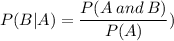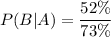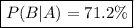Answer:
71.2%
Explanation:
The probability of events A and B happening together is
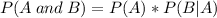
Now, the event A is costumers buying a wedding dress and its probability is
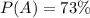 .
.
And the probability that a costumer gets a wedding dress AND a veil is
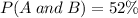
Therefore, the probability
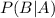 that a costumer who gets a wedding dress also gets a veil is
that a costumer who gets a wedding dress also gets a veil is