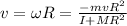a)
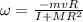
b)
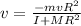
Step-by-step explanation:
a)
Since there are no external torques acting on the system, the total angular momentum must remain constant.
At the beginning, the merry-go-round and the girl are at rest, so the initial angular momentum is zero:
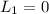
Later, after the girl throws the rock, the angular momentum will be:
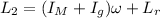
where:
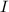 is the moment of inertia of the merry-go-round
is the moment of inertia of the merry-go-round
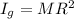 is the moment of inertia of the girl, where
is the moment of inertia of the girl, where
M is the mass of the girl
R is the distance of the girl from the axis of rotation
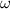 is the angular speed of the merry-go-round and the girl
is the angular speed of the merry-go-round and the girl
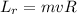 is the angular momentum of the rock, where
is the angular momentum of the rock, where
m is the mass of the rock
v is its velocity
Since the total angular momentum is conserved,
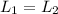
So we find:
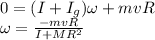
And the negative sign indicates that the disk rotates in the direction opposite to the motion of the rock.
b)
The linear speed of a body in rotational motion is given by
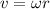
where
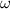 is the angular speed
is the angular speed
r is the distance of the body from the axis of rotation
In this problem, for the girl, we have:
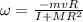 is the angular speed
is the angular speed
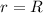 is the distance of the girl from the axis of rotation
is the distance of the girl from the axis of rotation
Therefore, her linear speed is: