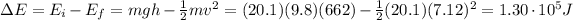Question

A parachutist of mass 20.1 kg jumps out of an airplane at a height of 662 m and lands on the ground with a speed of 7.12 m/s. The acceleration of gravity is 9.8 m/s 2 . How much energy was lost to air friction during this jump

Answer 1

`1.30\cdot 10^5 J`

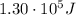
Step-by-step explanation:

The energy lost due to air friction is equal to the mechanical energy lost by the parachutist during the fall.

The initial mechanical energy of the parachutist (at the top) is equal to his gravitational potential energy:

`E_i=mgh`

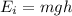
where

m = 20.1 kg is his mass

`g=9.8 m/s^2` is the acceleration due to gravity

h = 662 m is the initial heigth

The final mechanical energy (at the bottom) is equal to his kinetic energy:

`E_f=(1)/(2)mv^2`

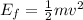
where

v = 7.12 m/s is the final speed of the parachutist

Therefore, the energy lost due to air friction is:

`\Delta E=E_i-E_f=mgh-(1)/(2)mv^2=(20.1)(9.8)(662)-(1)/(2)(20.1)(7.12)^2=1.30\cdot 10^5 J`