Question

A car starts from rest and moves around a circular track of radius 34.0 m. Its speed increases at the constant rate of 0.470 m/s2. (a) What is the magnitude of its net linear acceleration 16.0 s later

Answer 1

The magnitude of net linear acceleration of the car after 16 s later is
`1.72\ m/s^2`.

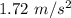Step-by-step explanation:

It is given that,

Initial speed of the car, u = 0 (at rest)

Radius of the circular track, r = 34 m

Acceleration of the car,
`a=0.47\ m/s^2`

We need to find the magnitude of its net linear acceleration 16.0 s later. It is equal to the resultant of radial and linear acceleration. The linear speed of the car after 15 seconds. So,

`v=u+at\\\\v=0+at\\\\v=0.47* 16\\\\v=7.52\ m/s`

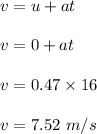
The radial acceleration of the car is given by :

`a'=(v^2)/(r)\\\\a'=((7.52)^2)/(34)\\\\a'=1.66\ m/s^2`

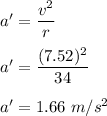
So, net acceleration of the car is given by :

`a_n=√(a^2+a'^2) \\\\a_n=√((0.47)^2+(1.66)^2) \\\\a_n=1.72\ m/s^2`

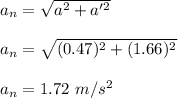
So, the magnitude of net linear acceleration of the car after 16 s later is
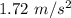`1.72\ m/s^2`. Hence, this is the required solution.