Question

Use the method of cylindrical shells to find the volume V generated by rotating the region bounded by the given curves about the specified axis. y = x3, y = 8, x = 0; about x = 5

Answer 1

V ≅ 8980 vu

Explanation:

According to the method of cylindrical shells V=πR²h, where R² (f(x)₂-f(x)₁), h=dx, f(x)₂=8 and f(x)₁=x³, then

V=π(8-x³)²h ⇒ dV=π(64-16x³+x⁶)dx integrating on both sides

∫dV = π∫(64-16x³+x⁶)dx = 64∫dx-16∫x³dx+∫x⁶dx ⇒

`V=\pi (64x-4x^(4)+(x^(7))/(7))`

`V=\pi (64*5-4*5^(4)+(5^(7) )/(7))=\pi(320-2500+(78125)/(7))\\ V=(\pi )/(7)(2240-17500+78125)`

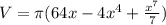
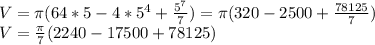
V ≅ 8980 vu

; evaluated to 0 ≤ x ≤ 5