Answer:
The probability of selecting a sample mean of 13 or larger from this population is 0.0228
Explanation:
A researcher selects a sample of 49 participants from a population with a mean of 12 and a standard deviation of 3.5.
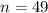
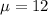
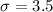
We are supposed to find the probability of selecting a sample mean of 13 or larger from this population i.e.
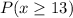
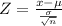
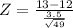
Z=2
Refer the z table
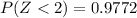
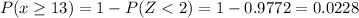
Hence the probability of selecting a sample mean of 13 or larger from this population is 0.0228