Question

after leaving the runway, a plane's angle of ascent is 16 degree and its speed is 267 feet per second. How many minutes will it take for the airplane to climb to a height of 12,500 feet?

Answer 1

The time taken for the airplane to climb to a height of 12,500 feet is 2.83 minutes.

Step-by-step explanation:

Given that,

Angle of the plane of ascent,
`\theta=16^(\circ)`

Initial speed of the plane, u = 267 ft/s

We need to find the time taken for the airplane to climb to a height of 12,500 feet. First lets find the vertical speed of the plane.

`u_y=u\ \sin\theta\\\\u_y=267* \ \sin(16)\\\\u_y=73.59\ ft/s`

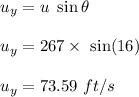
Let t is the time taken for the airplane to climb to a height of 12,500 feet. The speed of an object is given by :

`u=(d)/(t)\\\\t=(d)/(u)\\\\t=(12500\ ft)/(73.59\ ft/s)\\\\t=169.86\ seconds\\\\t=2.83\ min`

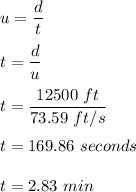
So, the time taken for the airplane to climb to a height of 12,500 feet is 2.83 minutes. Hence, this is the required solution.