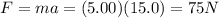Question

A 5.00 kg crate is suspended from the end of a short vertical rope of negligible mass. An upward force F(t) is applied to the end of the rope, and the height of the crate above its initial position is given by y(t) = (2.80 m/s)t + (0.61 m/s³)t³.

What is the magnitude of the force F when 4.10 s?
Is the magnitude's unit N but the system doesn't accept it?

Answer 1

75 N

Step-by-step explanation:

In this problem, the position of the crate at time t is given by

`y(t)=2.80t+0.61t^3`

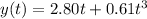
The velocity of the crate vs time is given by the derivative of the position, so it is:

`v(t)=y'(t)=(d)/(dt)(2.80t+0.61t^3)=2.80+1.83t^2`

Similarly, the acceleration of the crate vs time is given by the derivative of the velocity, so it is:

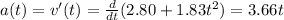`a(t)=v'(t)=(d)/(dt)(2.80+1.83t^2)=3.66t` [m/s^2]

According to Newton's second law of motion, the force acting on the crate is equal to the product between mass and acceleration, so:

`F(t)=ma(t)`

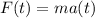
where

m = 5.00 kg is the mass of the crate

At t = 4.10 s, the acceleration of the crate is

`a(4.10)=3.66\cdot 4.10 =15.0 m/s^2`

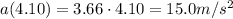
And therefore, the force on the crate is:

`F=ma=(5.00)(15.0)=75 N`