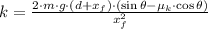Question

a block initially at rest has a mass m and sits on a plane incline at angle. it slides a distance d before hitting a spring and compresses the spring by a mazimum distance of xf. If the coefficient of kinetic friction between the plane and block is uk, then what is the force constant of the spring?

Answer 1

`k = (2\cdot m \cdot g \cdot (d+x_(f))\cdot (\sin \theta - \mu_(k)\cdot \cos \theta))/(x_(f)^(2))`

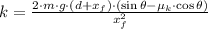
Step-by-step explanation:

Let assume that spring reaches its maximum compression at a height of zero. The system is modelled after the Principle of Energy Conservation and the Work-Energy Theorem:

`U_(g,A)=U_(k,B) + W_(f)`

`m\cdot g \cdot (d + x_(f))\cdot \sin \theta = (1)/(2)\cdot k \cdot x_(f)^(2)+\mu_(k)\cdot m \cdot g \cdot (d+x_(f))\cdot \cos \theta`

`m\cdot g \cdot (d + x_(f))\cdot (\sin \theta-\mu_(k)\cdot \cos \theta) = (1)/(2)\cdot k \cdot x_(f)^(2)`

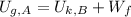
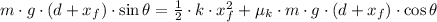
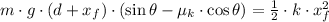
The spring constant is cleared in the expression described above:

`k = (2\cdot m \cdot g \cdot (d+x_(f))\cdot (\sin \theta - \mu_(k)\cdot \cos \theta))/(x_(f)^(2))`