Question

A wad of clay of mass m1 = 0.49 kg with an initial horizontal velocity v1 = 1.89 m/s hits and adheres to the massless rigid bar which supports the body of mass m2 = 2.13 kg, which can be assumed to be a particle. The pendulum assembly is freely pivoted at O and is initially stationary. The distance L = 0.90 m. Determine the angular velocity ω of the combined body just after impact. Why is linear momentum of the system not conserved?

Answer 1

The angular velocity just after collision is given as

`\omega = 0.23 rad/s`

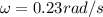
At the time of collision the hinge point will exert net external force on it so linear momentum is not conserved

Step-by-step explanation:

As per given figure we know that there is no external torque about hinge point on the system of given mass

So here we will have

`L_i = L_f`

now we can say

`m_1v_1(L)/(2) = (m_2L^2 + m_1((L)/(2))^2)\omega`

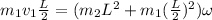
so we will have

`0.49(1.89)(0.45) = (2.13(0.90)^2 + 0.49(0.45)^2)\omega`

`\omega = 0.23 rad/s`

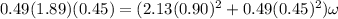
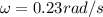
Linear momentum of the system is not conserved because at the time of collision the hinge point will exert net external force on the system of mass

So we can use angular momentum conservation about the hinge point