Question

Kayla wants to find the width, AB, of a river. She walks along the edge of the river 90 ft and marks point C. Then she walks 72 ft further and marks point D. She turns 90° and walks until her location, point A, and point C are collinear. She marks point E at this location, as shown.

Can Kayla conclude that ∆ABC and ∆EDC are similar? Why or why not? Suppose DE = 54 ft. What is the width of the river? Round to the nearest foot. Provide all work.

Answer 1

Part a: The triangles ∆ABC and ∆EDC are similar by AA similarity rule.

Part b: The width of AB is 67.5 feet

Step-by-step explanation:

Part a: We need to prove that the two triangles ABC and EDC are similar.

To prove the triangles are similar, then their angles must be similar.

Thus, we have,

∠DCE and ∠BCA are similar (vertical angles)

∠CDE and ∠CBA are similar (right angles)

∠B and ∠A are similar

Hence, the triangles ∆ABC and ∆EDC are similar by AA similarity rule.

Part b: We need to determine the width of AB

Since, the triangles are similar, then their corresponding lengths are proportional.

Thus, we have,

`(DE)/(AB) =(DC)/(CB)`

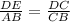
where
`DE=54 ft`,
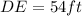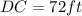`DC=72 ft` and
`CB=90ft`

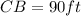
Substituting these values, we get,

`(54)/(AB) =(72)/(90)`

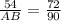
Multiplying both sides by 90, we get,

`(4860)/(AB)=72`

`(4860)/(72)=AB`

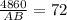
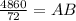
Dividing, we have,

`67.5=AB`

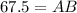
Thus, the width of the river AB = 67.5 feet