Question

At a point on the ground 24 ft from the base of a​ tree, the distance to the top of the tree is 4 ft more than 3 times the height of the tree. Find the height of the tree.

Answer 1

Therefore,

The height of the tree is 7 ft.

Explanation:

Consider a diagram shown below such that

Let,

AB = h = height of tree

'C' is a point on the ground 24 ft from the base 'B' of a​ tree

BC = 24 ft

The distance to the top of the tree is 4 ft more than 3 times the height of the tree

AC = 4 + 3h

To Find:

AB = h = ? ( height of tree)

Solution:

In Right Angle Triangle ABC by Pythagoras theorem we have

`(\textrm{Hypotenuse})^(2) = (\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)`

`AC^(2)=AB^(2)+BC^(2)`

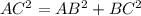
Substituting the values we get

`(4+3h)^(2)=h^(2)+24^(2)`

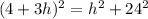
Using (A+B)²=A²+2AB+B² we get

`16+24h+8h^(2)=h^(2)+24^(2)`

`8h^(2)+24h-560=0`

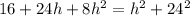
Dividing through out by 8 we get

`h^(2)+3h-70=0`

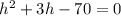
Which is a quadratic equation, so on factorizing we get

`(h+10)(h-7)=0\\h+10 =0\ or\ h-7 =0\\h= -10\ or\ h =7`

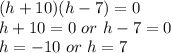
h cannot be negative therefore ,

`h = 7\ ft`

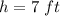
Therefore,

The height of the tree is 7 ft.