To solve this problem we will apply the concepts related to the balance of energy and forces. For the first part we will equalize the potential energy and the kinetic energy with which we can find the speed of the body. Later we will use the balance of forces that put the body in equilibrium to find the tension of the spring.
Our values are defined as,
m = 0.2 kg
r = 2.1 m
PART A) Equating potential energy at the start to kinetic energy at the lowest point:
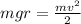
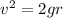
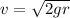
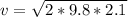
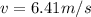
Therefore the velocity of the potato at the lowest point of its motion is 6.41m/s
PART B) Now, equating the forces to get the tension required:

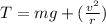
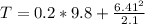
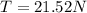
Therefore the Tension on the spring at this point is 21.52N