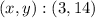Question

Which of the following coordinate points is the point of intersection of these two lines? y - 6x = -4 y - 2x = 8

Answer 1

For this case we have a system of two equations with two variables:

`y-6x = -4\\y-2x = 8`

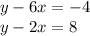
Rewriting the system we have:

`y = 6x-4\\y = 2x + 8`

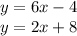
Equaling the equations we have:

`6x-4 = 2x + 8`

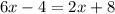
Subtracting 2x from both sides of the equation we have:

`6x-2x-4 = 8\\4x-4 = 8`

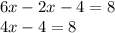
Adding 4 to both sides of the equation we have:

`4x = 8 + 4\\4x = 12`

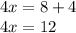
Dividing by 4 on both sides of the equation we have:

`x = \frac {12} {4}\\x = 3`

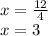
We find the value of the variable y:

`y = 6x-4 = 6 (3) -4 = 18-4 = 14`

Thus, the system solution is:

`(x, y) :( 3,14)`

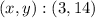
Answer:

`(x, y) :( 3,14)`