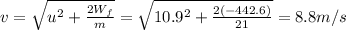a) -442.6 J
b) 8.8 m/s
Step-by-step explanation:
a)
The work done by the friction force is equal to:
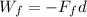
where
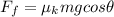 is the frictional force on the box, where
is the frictional force on the box, where
 is the coefficient of friction
is the coefficient of friction
m = 21 kg is the mass of the box
 is the acceleration due to gravity
is the acceleration due to gravity
 is the angle of the ramp
is the angle of the ramp
The negative sign is due to the fact that the frictional force is opposite to the motion of the box
d is the length of the ramp
So the work can be rewritten as
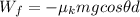
Here we know that the grade of the ramp, which is the ratio between height and horizontal length, is 0.7:
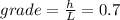
This means that
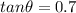
So we find the angle:
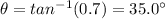
We also know that the height of the ramp is
h = 3.14 m
So we can find the length of the ramp:
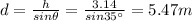
Therefore, the work done by friction is
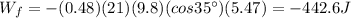
b)
The final speed of the box can be found by using the law of conservation of energy. In fact, the initial kinetic energy of the box (at the bottom) + the work done by friction must be equal to the final kinetic energy of the box, as it reaches the ground after leaving the platform.
So we can write:

where:
u = 10.9 m/s is the initial speed of the box
m = 21 kg is the mass of the box
 is the work done by friction
is the work done by friction
 is the final speed of the box as it reaches the ground
is the final speed of the box as it reaches the ground
Solving for v, we find: