Question

Which statement about the following equation is true?


2x2 – 9x + 2 = –1

Answer 1

Option C

Explanation:

The complete question is in the attachment.

The given equation is

`2 {x}^(2) - 9x + 2 = - 1`

We rewrite in standard form to get;

`2 {x}^(2) - 9x + 3 = 0`

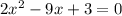
Compare to

`a {x}^(2) + bx + c = 0`

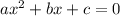
we have a=2, b=-9 and c=3.

We substitute into the formula for the discriminant:

`D= {b}^(2) - 4ac`

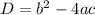
We substitute to get:

`D= {( - 9)}^(2) - 4 * 2 * 3`

`D=81- 24 = 57`

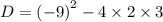
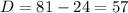
Since the discriminant is greater than zero, there are two real roots.