Question

You want to use the idea of electromagnetic induction to make the bulb in your small flashlight glow; it glows when the potential difference across it is 1.5 V. You have a small bar magnet and a coil with 100 turns, each with area 2.9 × 10−4m2. The magnitude of the B⃗ field at the front of the bar magnet's north pole is 3.6×10−2 T and reaches 0 T when it is about 4.0 cm away from the pole.

a) With what speed should you move the magnet to make the bulb light?
b) Can you make the bulb light? (yes/no/need more data)

Answer 1

a) 57.5 m/s

b) Yes

Step-by-step explanation:

a)

According to Faraday-Newmann-Lenz's law, the electromotive force induced in the coil due to the change in magnetic flux through it is given by:

`\epsilon=-(N \Delta \Phi)/(\Delta t)`

where

N is the number of turns in the coil

`\Delta \Phi` is the change in magnetic flux

`\Delta t` is the time interval

The change in magnetic flux can be written as

`\Delta \Phi = A\Delta B`

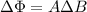
where

A is the area of the coil

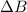`\Delta B` is the variation of the strength of the magnetic field

Re-writing the equation,

`\epsilon=-(NA\Delta B)/(\Delta t)`

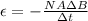
To make the bulb glowing, the induced emf must be:

`\epsilon=1.5 V`

And we also have:

N = 100

`\Delta B=0 T-3.6\cdot 10^(-2) T=-0.036 T`

`A=2.9\cdot 10^(-4) m^2`

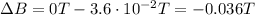
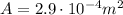
So we can find the maximum time required to induce this emf:

`\Delta t=-(NA\Delta B)/(\epsilon)=-((100)(2.9\cdot 10^(-4))(-0.036))/(1.5)=6.96\cdot 10^(-4) s`

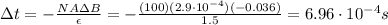
Since the length to cover in this time is

L = 4.0 cm = 0.04 m

The speed should be

`v=(L)/(t)=(0.04)/(6.96\cdot 10^(-4))=57.5 m/s`

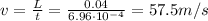
b)

Yes: if the coil is moved at a speed of 57.7 m/s, then the potential difference induced in the bulb will be 1.5 V, which is enough to make the bulb glowing.