Question

A 2.26 cm tall object is placed in 18.6 cm in front of a convex lens. The focal length

is 35.8 cm. How far is the image from the lens?

Answer 1

the image is -38.7 cm from the lens

Step-by-step explanation:

We use the lens equation which says

`$(1)/(u)+(1)/(v)=(1)/(f) $`

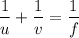
where
`u` is the distance to the object,
`v` is the distance to the image, and
`f` is the focal length.

Now, in our case

`u =18.6cm`,

`v= 35.8cm`,

`f = 35.8cm`;

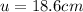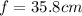therefore,

`$(1)/(18.6)+(1)/(v)=(1)/(35.8) $`

`$(1)/(v)=(1)/(35.8)-(1)/(18.6) $`

`\boxed{v=-38.7cm}`

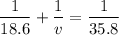
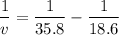
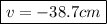
where the negative sign indicates that the image is virtual and on the same side of the lens as the object.