Question

Cot-1(-radical3)
find exact value in radians

Answer 1

θ = 5π/6 or 11π/6

Explanation:

It is required to find the value of
`Cot^(-1)(-√(3) )`

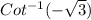
Let
`\theta = Cot^(-1)(-√(3) )`

So, cot θ = -√3 ⇒ tan θ = 1/cot θ = -1/√3

So, from the basic angles, we should know that

tan 30 = 1/√3 ⇒ Cot 30 = √3

But the given cot function is negative, so the required angle lies at the second quarter or at the fourth quarter.

So, θ = -30°

OR θ = 330° or 150°

converting to radians by multiplying at π/180

∴ θ = 330 * π/180 = 11π/6

Or θ = 150 * π/180 = 5π/6

So, θ = 5π/6 or 11π/6